cs101 ОП / Basics of programming ENG

1[olymp-1.pas] Caesar’s cipher is that each letter of the original string is replaced by the third letter after it in the alphabet, which is considered to be written in a circle (all characters of the text are Latin and uppercase).

* Make the same task with the next difference: the shift of the letters has to be not at 3 positions, but at k positions. If k has a negative value it means the shift to the left, a positive one - to the right.

Example:

3
hello earth
>>> khoor hduwk

2 (П.84).[olymp-2.pas] A sequence of N positive integers are given (input). You need to select and print two numbers among them so that their sum is odd, and the product is divided by 5 and at the same time it is maximum as possible. The numbers you will find may be displayed in any order. If there are several suitable pairs, you can choose any of them. If there are no suitable pairs -so output 0.

Example:

5
1
2
3
4
5
Output:
4 5

Comments: From 5 numbers you can make 10 pairs. In this case, two pairs satisfy the conditions: (2, 5) and (4, 5). The sums of numbers in these pairs (7 and 9) are odd, and the products (10 and 20) are divided by 5. Of these pairs, the pair with the largest product is selected.

3.[olymp-3.pas] Find the sum of all numbers from 1 to a given n that have exactly five divisors. The 1 and n itself are among its divisors.

Examples:

50 >>> 16
200 >>> 97
2015 >>> 722

4.[olymp-4.pas]N children are in a circle (picture).They are numbered from 1 to N. In turn every third person starts to leave the circle. This continues until the last person remains in the circle. Determine his number.

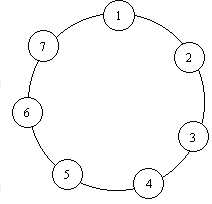
Examples:

7
3, 6, 2, 7, 5, 1 would leave him in turn
the result is 4

5 (86).[olymp-5.pas] A sequence of N positive integers is given. You are to determine the number of triples of elements (a_i, a_j, a_k) of this set in which 1 <= i < j <k <=N and the sum of these elements is a multiple of 7 (кратна 7) and odd.

Note: It will be better to write a program, which will be effective both in time and in memory. (without arrays).

Examples:

Input data:
7 
8 
11 
14 
15 
2 
4 
7
output data:
2
* in the sequence of 7 numbers there are two triples: (8, 11, 2) и (15, 2, 4).

6. [olymp-6.pas] The king of Flatland decided to cut down some trees growing in front of his palace. The trees in front of the king’s palace are planted in a rows, in general n trees grow there, the distances between neighboring trees are the same.

After felling, m trees should remain in front of the palace, and the distances between neighboring trees should be the same. Help the king find out how many ways there are to cut down trees.

It is required to write a program that will determine how many methods exist for cutting some of the n trees so that after cutting there are m trees and the neighboring trees are equally spaced from each other. m and n are entered.

Comments: If we arbitrarily designate the initial arrangement of trees in front of the palace as “TTTTT”, then the possible results after cutting are as follows: “TTT ..”, “.TTT.”, “..TTT”, “T.T.T”.

Example:

1	
5 
3
Output:
4

7. [olymp-7.pas] Fixed points. A permutation P [1..n] of size n is a set of numbers from 1 to n arranged in a certain order. Moreover, it must be present exactly once each of these numbers. Examples of permutations are 1,3,4,5,2 (for n = 5) and 3,2,1 (for n = 3), and, for example, 1,2,3,4,5,1 is not a permutation since the number 1 occurs twice.

The number i is called a fixed point for the permutation P if P [i] = i. For example, in the permutation 1,3,4,2,5 there are exactly two fixed points: 1 and 5, and the permutation 4,3,2,1 has no fixed points.

Two numbers are given: n and k. Find the number of permutations of size n with exactly k fixed points. n (1 ≤ n ≤ 9) and k (0 ≤ k ≤ n).

Example:

Input:            Output:
1	5 2	      20
2	9 6	      168
3	2 1	      0
4	9 0	      133496