Лабораторная работа №2. Решение статической задачи теории упругости средствами FreeFem++
Требуемые условия завершения
Чтобы убедиться в правильности построения области, используем
Строим графики:
Савицкий - 1
Терентьев - 2
Узлов - 3
Филатов - 4
Открыто с: пятница, 28 февраля 2025, 00:00
Срок сдачи: пятница, 7 марта 2025, 00:00
Рассмотрим задачу для тела, изображённого на рисунке 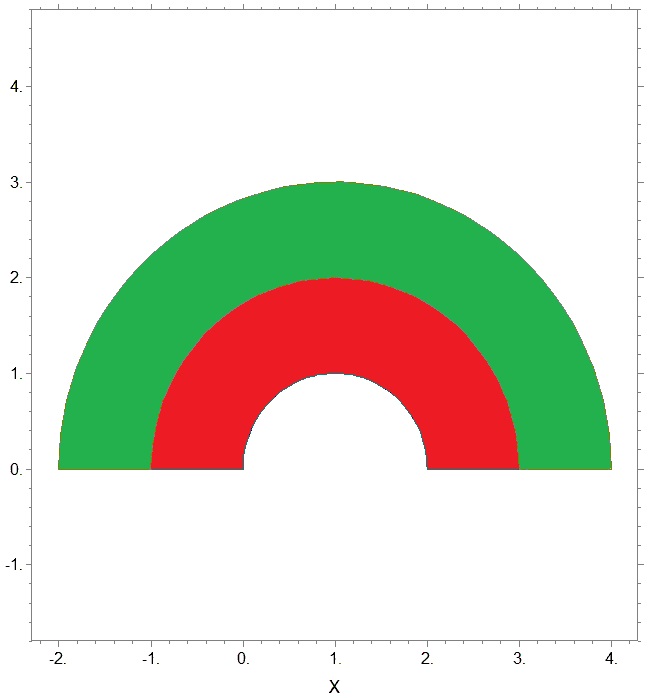
Область состоит из двух материалов. Правый нижний отрезок [2, 4] жестко закреплён, на левом [-2, 0] - задана нагрузка. Область состоит из двух материалов. Внешнее кольцо состоит из стали, внутреннее - из меди. Задачу решает код в файле static.edp. Программа FreeFem написана на языке C++ и синтаксис входного файла во многом на него похож.
Начинается он с определения вещественных констант. Определим модули Юнга и коэффициенты Пуассона для стали и для меди.
real Esteel = 210e3; real nuSteel = 0.3; real Ecopper = 110e3; real nuCopper = 0.35;Как видно, переменная определяется так же, как и в языке C++ (указываем тип переменной, указываем её имя, задаём значение). Далее определяем коэффициенты Ляме для двух материалов.
real lambdaSteel = Esteel*nuSteel / ((1+nuSteel)*(1-2*nuSteel)); real muSteel = Esteel / (2*(1+nuSteel)); real lambdaCopper = Ecopper*nuCopper / ((1+nuCopper)*(1-2*nuCopper)); real muCopper = Ecopper / (2*(1+nuCopper));Далее идёт построение контуров области, определение внешних границ и границы раздела между двумя материалами.
border C1(t=0, pi){x=3*cos(t); y=3*sin(t); label=1;} // внешняя полуокружность
border C21(t=-3, -2){x=t; y=0; label=21;}
border C22(t=-2, -1){x=t; y=0; label=22;}
border C3(t=0, pi){x=-cos(t); y=sin(t); label=3;} // внутренняя полуокружность
border C41(t=1, 2){x=t; y=0; label=41;}
border C42(t=2, 3){x=t; y=0; label=42;}
border interface(t= 0,pi ){x=-2*cos(t); y=2*sin(t); label=5;} // граница раздела
В записи border C1(t=0, pi){x=3*cos(t); y=3*sin(t); label=1;}:
- Ключевое слово border используется для определения границы или части границы геометрической области;
- C1 - имя, которое присваивается данной границе. Вы можете выбрать любое имя;
t- параметр, который пробегает значения от0доpi;x=3*cos(t); y=3*sin(t);- это параметрическое уравнение кривой, которое описывает форму границы;- метка (
label) присваивает уникальный номер этой границе;
Далее создаётся конечноэлементная сетка для области
mesh Th = buildmesh(C1(50) + C21(5) + C22(5) + C3(50)+ C41(5) + C42(5)+ interface(50));Th -то имя переменной, которое будет хранить созданную сетку. Тип переменной — mesh, что означает, что это двумерная сетка. C1(50) - означает, что граница разбивается на 50 сегментов, которые в дальнейшем будут использованы при разбиении области.
Чтобы убедиться в правильности построения области, используем
plot(Th, wait=true, ps="mesh_with_materials.eps");Далее переходим к слабой постановке задачи
fespace Vh(Th, P2); // определяет пространство квадратичных конечных элементов на сетке Th. Vh u, v; // неизвестные функции Vh uu, vv; // пробные функцииОпределяем деформации
// Macro real sqrt2=sqrt(2.); macro epsilon(u1,u2) [dx(u1),dy(u2),(dy(u1)+dx(u2))/sqrt2] // // The sqrt2 is because we want: epsilon(u1,u2)'* epsilon(v1,v2) = epsilon(u): epsilon(v) macro div(u,v) ( dx(u)+dy(v) ) //Определяем неоднородные механические парамеры
Vh lambda= x*x+y*y < 4 ? lambdaCopper : lambdaSteel; Vh mu= x*x+y*y < 4 ? muCopper : muSteel;Записываем слабую постановку
solve lame([u, v], [uu, vv]) = int2d(Th)( lambda * div(u, v) * div(uu, vv) + 2.*mu * ( epsilon(u,v)' * epsilon(uu,vv) ) ) - int1d(Th, 21)( 1*vv ) - int1d(Th, 22)( 1*vv ) + on(41, u=0, v=0) + on(42, u=0, v=0) ;int1d - для задания поверхностной нагрузки, on - для задания закрепления.
Строим графики:
// Plot real coef=100; plot([u, v], wait=1, ps="lamevect.eps", coef=coef); // векторное поле // Move mesh mesh th1 = movemesh(Th, [x+u*coef, y+v*coef]); plot(th1,wait=1,ps="lamedeform.eps"); // деформированная сеткаГрафики напряжений
// деформации Vh exx = dx(u), eyy = dy(v), exy = (dy(u) + dx(v)) / 2; // напряжения Vh sxx = lambda * (exx + eyy) + 2*mu*exx; Vh syy = lambda * (exx + eyy) + 2*mu*eyy; Vh sxy = 2*mu*exy; // графики plot(sxx, wait=true, value=true, fill=true, cmm="Sigma_xx"); plot(syy, wait=true, value=true, fill=true, cmm="Sigma_yy"); plot(sxy, wait=true, value=true, fill=true, cmm="Sigma_xy");Варианты:
Савицкий - 1
Терентьев - 2
Узлов - 3
Филатов - 4
- 1 марта 2025, 07:54
- 1 марта 2025, 08:54