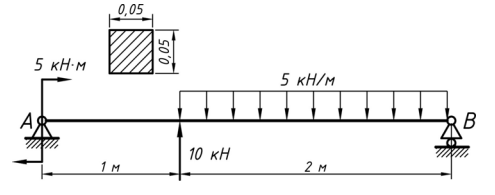
Решение задачи:

В Ansys Main Menu выбираем пункт Preferences, после чего в появившемся окне устанавливаем флажок на пункте Structural, определяя тем самым тип планируемого анализа.

1. Выбор типа конечных элементов. Раскрываем список Preprocessor, последовательно выбираем Element Type и Add/Edit/Delete. В появившемся окне нажимаем кнопку Add. Открывается окно библиотеки конечных элементов. В левом списке выбираем Beam, в правом - 2 node 189. Подтверждаем свой выбор кнопкой Ok и затем закрываем окно Element Types. Чтобы ограничиться плоской балкой, нужно оставить в узле три степени свободы - перемещения в направлении осей x и y, a также поворот rotz. Для этого в командной строке вводим

   KEYOPT, 1, 5, 1 ! Плоское поведение (XY-плоскость)

2. Далее задаём свойства материала. Выбираем в главном меню пункт Material Props->Material Models. В появившемся окне в списке справа выбираем пункт Structural->Linear->Elastic->Isotropic. Затем в появившемся окне задаём свойства EX = 2.1e11 (модуль Юнга), PRXY = 0.29 (коэффициент Пуассона). Также последнее действие можно выполнить при помощи командной строки, если ввести в неё команды

   MP, EX, 1, 2e11  ! Модуль упругости (сталь, 200 ГПа)
   MP, PRXY, 1, 0.3  ! Коэффициент Пуассона

3. Далее задаём свойства сечения. Выбираем в главном меню Sections->Beam-Common Sections. Выбираем Sub-Type (форму сечения), вводим значения B (0.05) и H (0.05).
4. Строим балку. Для этого указываем ключевые точки и по ним проводим линию

   K,1
   K,2,1
   K,3,3
   L,1,2
   L,2,3

5. Построим сетку конечных элементов. Выбираем в главном меню Preprocessor->Meshing->Mesh Tool. Нажимаем кнопку Set, соотнесённую с заголовком Lines. Выбираем линии и нажимаем Ok. Далее появится окно, в котором можно установить размер элементов. Далее в окне Mesh Tool нажимаем Mesh и выбираем все линии.
6. Открываем список Solution. Далее наложим граничные условия. Раскрываем список Solution->Define Loads->Apply->Structural->Displacement->On Nodes. Выбираем крайнюю левую точку, в появившемся окне нажимаем Ok, и выбираем степени свободы UX и UY 
   
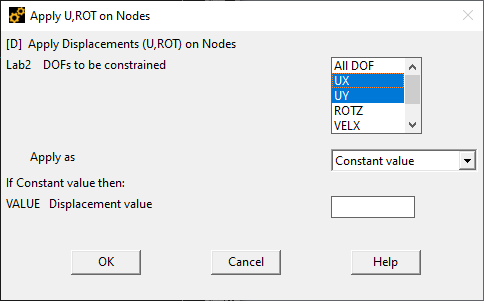
   То же самое делаем с крайней правой ключевой точкой, указывая только одну степень свободы UY.
7. Прикладываем момент. Раскрываем список Solution->Define Loads->Apply->Structural->Force/Moment->On Keypoints. Выбираем крайнюю левую точку, жмём Ok, в появившемся окне выбираем Lab – MZ и значение момента -5000 (направление - по часовой стрелке). Точно так же прикладываем сосредоточенную силу (вместо MZ выбираем FY).
8. Прикладываем распределённую нагрузку. Раскрываем список Solution->Define Loads->Apply->Structural->Pressure->On Beams. Выбираем все элементы, к которым прикладывается нагрузка, в поле VALI указываем её значение.
9. Решаем задачу. Solution->Solve->Current LS.
10. Читаем решение General PostProc->Read Results->First Set
11. Ищем реакции опор General PostProc->List Results->Reaction Solu ->All Items
12. Строим эпюру перерезывающей силы. Сперва создаём Element Table. Выбираем General PostProc->Element Table->Define Table. В появившемся окне нажимаем Add, в новом окне вводим Lab = MI, в левом списке выбираем пункт By sequence num, в списке справа - SMISC, , в окне снизу - SMISC, 2. Строим ещё одну таблицу MJ и выбираем SMISC, 15. Далее выбираем General PostProc -> Plot Results -> Line Elem Res, выбираем в качестве LABI - MI, в качестве LABJ - MJ, жмём OK.
13. Точно так же строим эпюру перерезывающей силы. Для таблицы QI выбираем SMISC, 5, для QJ - SMISC, 18.