Конечноэлементные технологии и новые материалы (факультатив)

Рассмотрим упругое тело, имеющее форму, изображённую на рисунке:

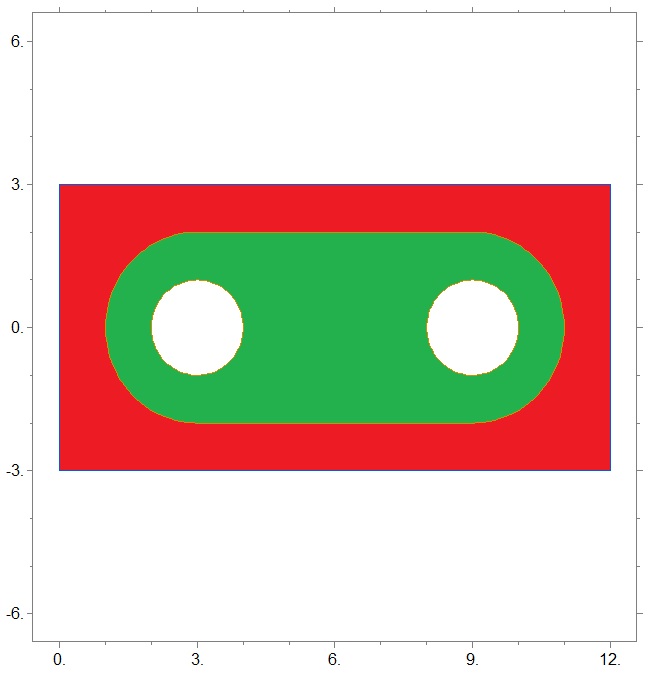
1. Выбираем Preferences -> Structural;
2. Выберем сперва тип элемента. Preprocessor -> Element Type -> Add/Edit/Delete -> Add -> Solid -> Quad 4 node 182. Закрываем окно выбора элементов;
3. Задаём свойства материалов. Считаем, что область состоит из двух материалов, красным цветом обозначена сталь, зелёным - медь. Выбираем Preprocessor -> Material Props -> Material Models. Для модели Material Model Number 1 выбираем в правом списке Structural -> Linear -> Elastic -> Isotropic. В появившемся окне вводим значения: EX = 2.1e11, PRXY = 0.29 (материальные константы для стали). Далее следует задать плотность материала. Для этого в том же самом окне Define Material Model Behavior выбираем в правом списке Density (плотность) и в появившемся окне вводим знасение DENS = 7.8e3. 
   Так как область состоит из двух материалов, нам следует задать свойства для второго материала. Для этого в том же окне Define Material Model Behavior открываем меню Material и выбираем пункт New Model, вводим в окне номер нового материала (2), нажимаем OK и точно так же для нового материала задаём значения EX = 1.2e11, PRXY = 0.33, DENS = 8.9e3;
4. Строим область. Сперва построим два прямоугольника. Preprocessor -> Modeling -> Create -> Areas -> Rectangle -> By Dimensions. В появившемся окне вводим X1, X2 = 0, 12, Y1, Y2 = -3,3. Строим меньший прямоугольник с параметрами  X1, X2 = 3, 9, Y1, Y2 = -2,2.
5. Строим круги Preprocessor -> Modeling -> Create -> Areas -> Solid Circle. В появившемся окне вводим WP X = 3, WP Y = 0, Radius = 2. Строим еще три круга с параметрами  WP X = 3, WP Y = 0, Radius = 1. Затем с параметрами WP X = 9, WP Y = 0, Radius = 2 и с параметрами WP X = 9, WP Y = 0, Radius = 1.
6. Воспользуемся теперь булевыми операциями. Сольём меньший прямоугольник с большими кругами. Выбираем Preprocessor -> Modeling -> Operate -> Booleans -> Add -> Areas. Выбираем на схеме три площади и нажимаем Ok.
7. Далее вычтем из большего прямоугольника вычтем получившийся овал. Preprocessor -> Modeling -> Operate -> Booleans -> Substract -> With Options -> Areas. Выбираем на схеме большой прямоугольник, нажимаем Ok, выбираем овал и нажимаем Ok. В появившемся окне выбираем KEEP2 = Kept
   
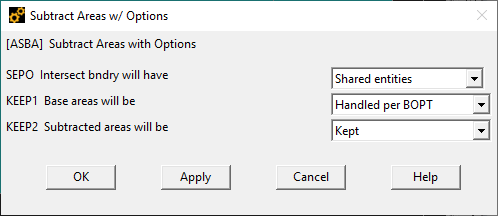
8. Далее вычитаем из большоги овала два меньших круга. Выбираем Preprocessor -> Modeling -> Operate -> Booleans -> Substract -> Areas. Выбираем нужные площади.
9. Связываем две области с созданными материалами : Preprocessor -> Meshing -> Mesh Attributes -> Picked Areas, выбираем на схеме площадь, нажимаем Ok и выбираем в окне номер материала. Проделываем эти действия для обеих площадей.
10. Выбираем Mesh Tool. Нажимаем в окне MeshTool кнопку Set, соответствующую Areas, выбираем площади и указываем размер элемента (например, 0.3). Нажимаем Mesh и указываем разбиваемые площади, жмём Ok.
11. Переходим в список Solution. Выбираем Analysis Type -> New Analysis -> Modal.
12. Выбираем Analysis Options, устанавливаем количеств мод равным семи.
13. Закрепляем левый и правый края прямоугольника. Solution -> Define Loads -> Apply -> Structural -> Displacement -> On Lines, выбираем линии и выбираем степени свободы.
14. Выбираем Solve -> Solution. Для просмотра результатов переходим в General Postrpoc. Частоты - Results Summary, формы колебаний - Results viewer.
15. Теперь произведём гармонический анализ. Построим для образца амплитудно-частотную характеристику (АЧХ). Амплитудно-частотная характеристика (Frequency response) - это зависимость апмлитуды вынужденных колебаний от частоты вынуждающей силы. Для этого выбираем Solution -> Analysis Type -> New Analysis. Выбираем Harmonic. Далее выбираем Solution -> Load Step Opts -> Freq and Substeps. Выбираем HARFRQ - от 0 до 150, NSUBST - 150.
16. Следует теперь определить вынуждающую нагрузку. Solution -> Define Loads -> Apply -> structural -> Pressure -> On Lines, указываем на схеме линию, нажимаем Ok и вводим интенсивность осциллирующей нагрузки (1e6).
17. Решаем задачу Solve -> Current LS
18. Заходим в TimeHist PostPro, нажимаем на кнопку Add Data -> DOF Solution -> Y-Component of displacement, нажимаем Ok и выбираем на схеме узел, амплитуду перемещения которого мы отображаем на графике, нажимаем в окне на кнопку Graph Data.

Варианты

Савицкий - 1
Терентьев - 2
Узлов - 3
Филатов - 4