Тематический план
-
-
Раздел 1. Изоморфизм. Цикломатика. Раскраски
Изоморизм графов. Инварианты графа. Проблема изоморфизма.
Цикломатика графа. Каркасы и разрезы. Пространства циклов и разрезов. Планарность. Гипотеза Хадвигера.
Раскраски графа. Хроматический многочлен графа. Внутренне и внешне устойчивые множества. Ядра графа. Функция Гранди.
Раздел 2. Спектры графов
Спектры графов. Оценки спектрального радиуса. Собственные подпространства. Связь спектра и структуры графа. Приложения спектральной теории графов в математике, физике, химии.
Раздел 3. Динамические графовые модели
Потоковые модели в динамических сетях. Задача о максимальном суммарном потоке в динамической периодической сети. Потоковая модель в сети с потребителями.
Ресурсные сети. Классификация ресурсных сетей по топологии. Пороговое значение. Потоки и предельные состояния в ресурсной сети. Аттракторы и их классификация.
-
- Три определения графа. Пути и циклы на графе. Леммы о простых и элементарных путях и циклах.
- Изоморфизм графов. Проблема изоморфизма.
- Инварианты графа.
- Какрасы и разрезы графа.
- Пространства циклов и разрезов.
- Планарные графы. Теоремы о раскрасках планарного графа.
- Гипотеза Хадвигера.
- Хроматический многочлен графа.
- Хроматическое число.
- Ядра графа. Функция Гранди.
- Оценки спектрального радиуса.
- Собственные подпространства.
- Алгебраическая звязность графа.
- Задача о максимальном суммарном потоке в динамической периодической сети.
- Потоковая модель в сети с потребителями.
- Классификация ресурсных сетей.
- Пороговое значение эргодической ресурсной сети.
- Потоки и предельные состояния в ресурсных сетях.
- Аттракторы и их классификация.
- Ресурсные сети с ограничениями на ёмкость вершин.
- Обратные задачи в ресурсных сетях.
- Три определения графа. Пути и циклы на графе. Леммы о простых и элементарных путях и циклах.
-
Контрольные вопросы:
- Являются ли следующие графы изоморфными?
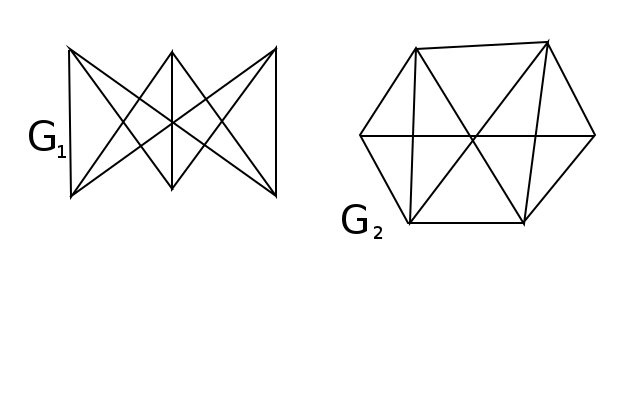
- Найдите инварианты \( \varphi(G), \varepsilon(G), \gamma(G), \varkappa(G) \)для графов \( G_1 \) и \( G_2 \)
- Являются ли следующие графы изоморфными?
-
Контрольные вопросы:
- Найдите минимальный разрез для следующего графа
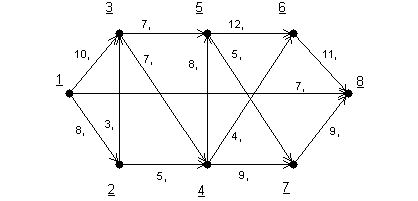
- Найдите базис пространства циклов графа
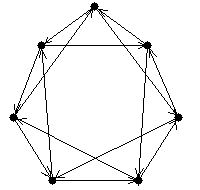
- Найдите минимальный разрез для следующего графа
-
Контрольные вопросы:
- Что означает равенство В + Г - Р = 2?
- Докажите указанное равенство для дерева.
- Является ли следующий граф планарным? Правильно ли он реализован?
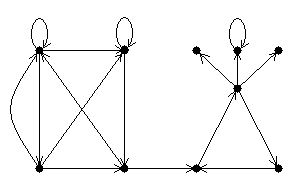
-
Контрольные вопросы:
- Сформулируйте гипотезу черырёх красок.
- Найдите хроматическое число и хроматический многочлен следующего графа
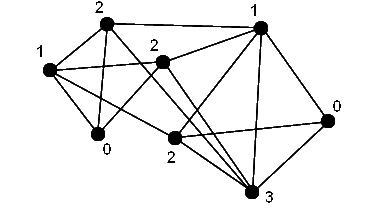
- Сформулируйте гипотезу черырёх красок.
-
Контрольные вопросы:
- Перечислите все внешне устойчивые множества графа \( G1 \) и все внутренне устойчивые множества графа \( G_2 \)
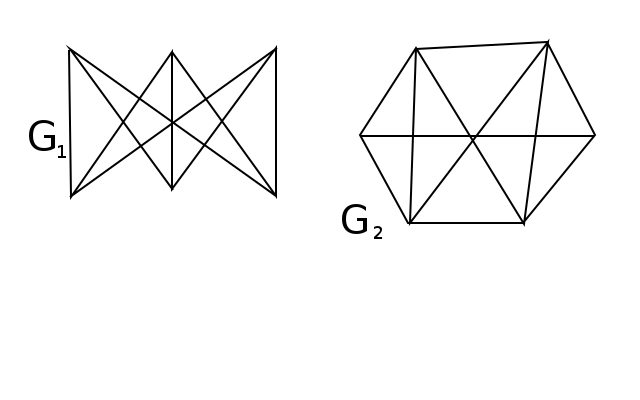
- Для следующего графа найдите ядро с наибольшим числом вершин
- Перечислите все внешне устойчивые множества графа \( G1 \) и все внутренне устойчивые множества графа \( G_2 \)
-
Примерные задания (по разделам)
Контрольная работа №1 (раздел 1, 15 баллов)
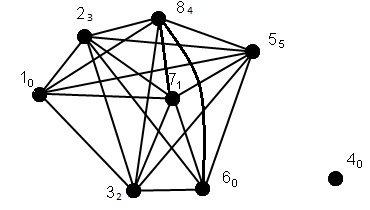
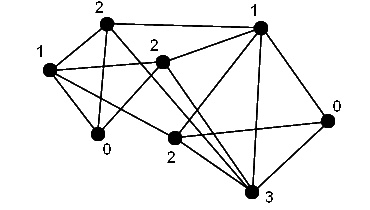
Для представленного на рисунке графа
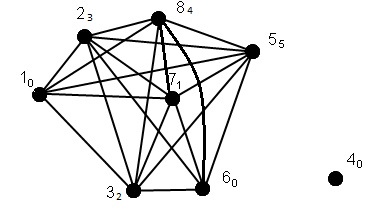
- Определите один из базисов пространства циклов.
- Найдите максимальную клику.
- Постройте хроматический многочлен.
- Определите, чему равны цикломатическое и хроматическое числа.
- Постройте ядро максимальной мощности.
Контрольная работа № 2 (раздел 2, 15 баллов)
- Граф G1 задан своей матрицей смежности A. Определите его спектральный радиус.
- Граф G1' получен из G1 стягиванием дуги (1,2). Определите спектральный радиус графа G1'.
- Граф G2 представлен на рисунке.
Найдите величину его алгебраической связности.
- Найдите собственное подпространство для алгебраической связности произведения графов G1G2.
-
Вариант 1.
- Для графа \( G_1 \) вычислить суммарный поток за 7 тактов.
- Для сети \( G_1 \) рассчитать максимально возможную суммарную величину потребления. Указать частный случай распределения потока при котором она достигается.
- Для ресурсной сети \( G_2 \) найти пороговое значение и предельное состояние для следующего начального Q(0)=(50,0,0,0,0,0,0,0,0,0).
\( G_1 \),
\( G_2 \).
Вариант 2.- Для графа \( G_1 \) вычислить суммарный поток за 7 тактов.
- Для сети \( G_1 \) рассчитать максимально возможную суммарную величину потребления. Указать частный случай распределения потока при котором она достигается.
- Для ресурсной
сети \( G_2 \) найти пороговое значение и предельное состояние для
следующего начального Q(0)=(40,0,0,0,0,0,0,0,0,0).
\( G_1 \),
\( G_2 \).